-Ray (quoted with permission)
“I don’t know where you get your delusions, laser brain.” -Princess Leia

Quick Summary
In order to match the dosing used in the Naeser studies (R, R) use the 96 LED Array:
1) for 353 seconds per spot
2) on 11 eleven different spots
3) on Monday, Wednesday, and Friday.
Dosing Formula: Energy (in Joules per cm2) = Power (in Watts per cm2) x time (in seconds)
Introduction
As many of you know I like to pick a pattern (or two) from the scientific literature to follow when I’m performing experiments on myself.
The best patterns for transcranial LLLT with LEDs are the two Naeser studies from 2011 (R) and 2014 (R).
The reason they are two of the best studies is that we can easily imitate them with VERY affordable LED arrays found on Amazon: 96 LED Array.
Let’s take a look and get some inspiration for our own experiments, shall we?
We shall!
Naeser 2011 and 2014
The two Naeser studies used LED arrays on 13 total brain injury victims which caused remarkable recovery of function years after the trauma.
Given the prevalence of CTE, TBI, PTSD, Alzheimer’s, age related cognitive decline, etc. this modality has the potential to dramatically improve the lives of millions of people.
And I’m gonna show you how to do it for $40 instead of $4,000!
Read on.
Array of Light
The LED arrays ultimately used (they started with something slightly different) in the two studies had 61 diodes.
52 of those diodes were 870 nanometer (nm) diodes and 9 were 633 nanometer diodes.
They looked a little something like this.

The little X in the middle of the array is made up of the 9 633nm diodes and the other LEDs constitute the 52 870nm diodes.
The 870nm and 633nm refer to the two different wavelengths of light emitted by the diodes.
What is a wavelength? It’s this.
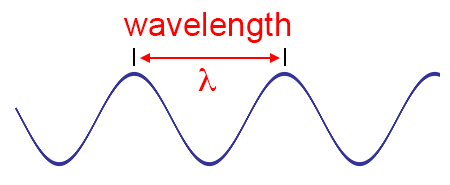
So, wavelength is the length from crest to crest (for our purposes).
What is a nanometer?
If you divide up a meter stick into a billion equal segments, each of those segments is one nanometer in length; ie. a nanometer is one billionth of a meter or another way of putting it is that 1,000,000,000 nanometers = 1 meter.
Anyway, the point is that the distance from crest to crest on a wave of light is miniscule and when it comes to LLLT, wavelength is one of our most important parameters.
The light must be certain wavelengths (870nm is a good one) in order to penetrate far enough and stimulate the proper electrons (through photoexcitation) in cytochrome c oxidase of the electron transport chain.
The 870nm diodes emitted 12.25 milliwatts (mW) of power each and the 633nm diodes emitted 1mW each.
“mW” stands for milliwatts which is 1/1000 of a Watt. Another way of putting it is that 1000 milliwatts = 1 Watt.
So, 52 of the 870nm diodes were emitting 12.25mW of power each.
That comes out to 52 x 12.25 = 637mW (my 6th grade math teacher said to always show my work!).
The 9 633nm diodes were emitting 1mW of power each.
That comes out to 9 diodes x 1mW per diode = 9mW total.
So, our total milliwatts of power is 637mW + 9mW = 646mW of power.
As you have likely surmised, the 870nm diodes are doing most of the work here and the 633nm diodes probably don’t have much of an effect (though they might have a small one!).
The Joule of the Nile
The dose they ultimately settled on in the two Naeser studies was 13 J/cm2.
One cm2 looks like this.
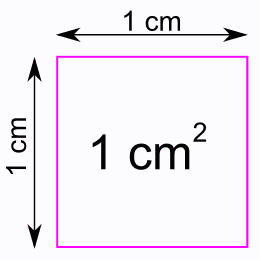
Now we’re gonna shoot some light at that square!

Light comes in individual wave-particles called photons.
Each photon carries a tiny amount of energy (for my fellow nerds out there the energy of a photon is represented by the Planck-Einstein relation E = hf…but this doesn’t concern us here.).
That energy is measured in units called Joules.
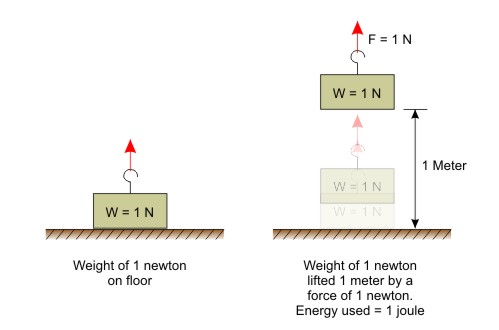
Energy measures the ability of something to do work.
Work is the ability to cause displacement in the direction of a force.
I basically think of work as the ability to cause movement or the ability to cause something to move.
You perform work on something when you make it move.
If I shove my little brother, I do some work.
If I shove him really hard, I do more work.
If I shove a massive MMA fighter, I get worked.

Easy, big fella.
In the case of LLLT, the photons from our LEDs are absorbed by electrons in mitochondria, cause them to become excited and jump to higher energy state, and therefore do extra work. Beautiful!
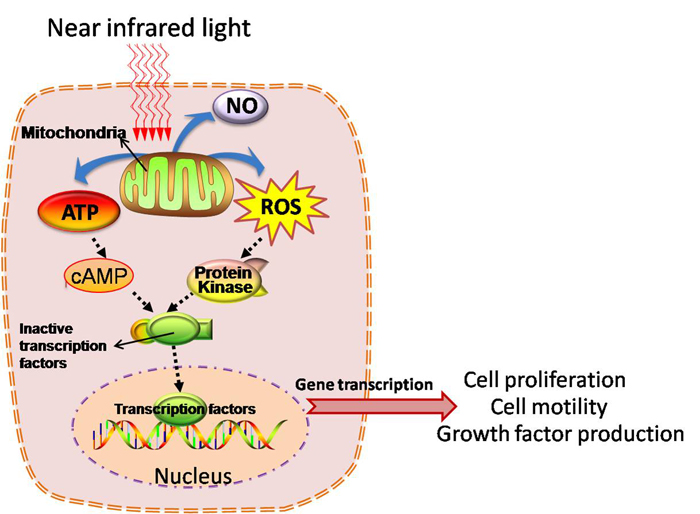
Give Me the Secret Formula!
The formula for calculating LLLT dose goes a little something like this:
Energy (in Joules per cm2) = Power (in Watts per cm2) x time (in seconds).
It can be rewritten as E(J) = P(W) x t(s) or E(J/cm2) = P(W/cm2) x t(s).
In the Naeser studies they settled on:
E(J) = 13.3 Joules/cm2
P(W) = .0222 Watts/cm2
t(s) = 600 seconds
So, we can set up our own equation and calculate our dose based on these numbers.
The Dose Makes The…Medicine
The 96 LED array (12 LEDs across and 8 LEDs up) that I recommend has 96 850nm diodes and each of them emit around 23 mW per diode.
This is according to Scott Roberts who is an electrical engineer that actually builds LLLT devices. R
Here he is.

Here’s a link to his excellent site on LLLT: heelspurs.com
The wavelength of the LEDs on our affordable array are 850nm which is very close to 870nm and should have extremely similar biological effects.
So, 96 LEDs at 23mW per LED gives us: 96 x 23 = 2,208 mW emitted for the whole array.
Remember, our equation uses Watts and not milliwatts. Thus, we need to translate our dose to Watts.
There are 1000mW in 1 Watt, therefore, 2208/1000 = 2.208 Watts for the whole array.
Nice!
Now, we need to figure out our dose per cm2 of the array.
How big is our whole array?

Well, I got out my trusty measuring tape and measured 10cm by 6cm (starting and ending at the edges of the LEDs).
Area equals length x width, so 10cm x 6cm gives us 60cm2 for the whole array.
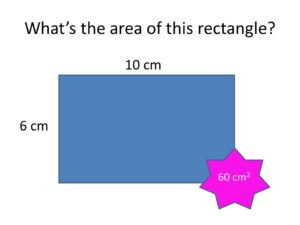
That gives us 2.208 Watts and 60cm2 for the whole array.
Now we need to figure out how much light 1 cm2 is getting.
Divide 2.208 by 60cm2 and we get .0368 W/cm2.
This is how many Watts of power each 1 cm square is getting at the surface of our skin.
As you’ll recall, our equation is Energy (in Joules per cm2) = Power (in Watts per cm2) x time (in seconds).
From the Naeser studies we know our desired energy (the ‘E’ part of our equation) is going to be 13 Joules per centimeter squared (I rounded) and we just calculated our power in Watts (.0368 W/cm2).
All we have to do now is determine our time in seconds and we’ll be good to go.
13 J/cm2 = .0368 W/cm2 x t(s)
Therefore, t(s) = 353 seconds.
There you have it!
E(J/cm2) = 13
P(W/cm2) = .0368
t(s) = 353
In order to match the dose from the Naeser studies we would want to use the 96 LED array for around 353 seconds or 5.89 minutes (353 seconds divided by 60 seconds per minute) per spot.
How Much Gets to Our Brain?
We have just calculated the dose at the level of our skin.
So, how much penetrates the skin, blood, bone, etc. and reaches the brain?
Estimates vary, but around 2% to 4% of this light likely reaches the brain.
If we go with 3% then we get a total .4 Joules per centimeter squared (13 Joules x .03).
This exactly matches the Naeser studies!
How Many Spots?
Now that we have the amount of time we need to spend per spot, we need to figure out which spots to laser.

They lasered 11 spots each day.
Here they are.

They used 6 LED arrays at a time and lasered for 10 minutes on 6 six different spots and then changed to 5 different spots and lasered those for 10 minutes.
Their total time under the LEDs was 20 minutes.
How Often?
They lasered three days a week: Monday, Wednesday, and Friday.
Also, make sure you push the LEDs past your hair and into your skin since hair blocks the light and pushing will increase penetration depth.

Aaaand…we are done.
Boom goes the dynamite!

Summary
Use the 96 LED array for 353 seconds per spot on 11 different spots per day on three days per week: Monday, Wednesday, and Friday.
This will get your dose pretty damn close to the two Naeser studies.
Enjoy your photon enhanced brain!

Until next time…LF Out.

11 Comments
Leave your reply.